Wheel Signatures
MSRI-UP 2022
Luis Gomez (University of Arkansas),
Loan Tran (San Francisco State University),
and Elijah Washington (Williams College)Research Assistant: Natasha Crepeau (U Washington)
Research Director: Professor Anne Shiu (Texas A&M)






Neural codes can be realized as collections of sets, where each set represents a neuron.We wish to explore the properties of the wheel, a type of non-convexity for a set of neural codes. In other words, if a code contains a wheel, then the realization of the code is forced to be open non-convex (but it can still be closed convex).
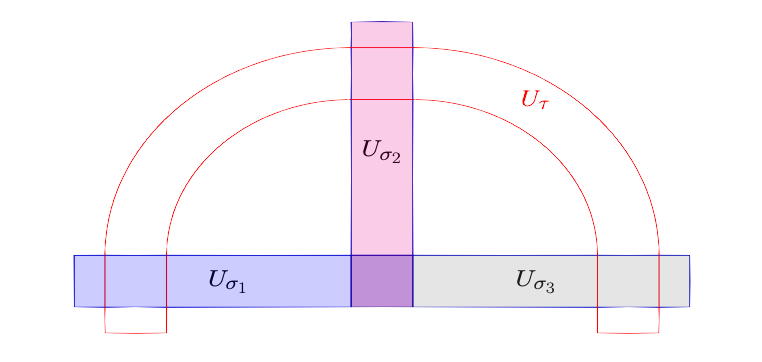
It is interesting to understand when these realizations are open convex. There are previous findings of different types of non-convexity for neural codes, i.e. wheels, partial wheels, wire wheels, and sprockets.We translate the conditions of these different types of non-convexity into conditions on the neural ideal which is generated by characteristic functions of codewords that are not contained in the code.These translations give rise to algebraic signatures for wheels and wheel variants within the neural ideal.
Sorry, the paper is not accessible to the public at this moment.
Contact Us
Here are some of the other MSRI-UP 2022 groups:
The Effect of Operations on the Deficiency of Chemical Reaction Networks